Research Group:
Speaker:
Khazhgali Kozhasov
Schedule:
Friday, January 12, 2018 - 14:30 to 16:00
Location:
A-133
Abstract:
Let  be the (projectivized) variety of real symmetric matrices with repeated eigenvalues. It is a well known fact that the codimension of
be the (projectivized) variety of real symmetric matrices with repeated eigenvalues. It is a well known fact that the codimension of  is two. Let
is two. Let  be a generic projective
be a generic projective 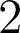 -plane in
-plane in  . We prove the sharp upper bound:
. We prove the sharp upper bound:
Moreover in the case when is taken to be random and uniformly distributed in the Grassmannian
we prove that the expected number of intersection points equals:
The proof involves the computation of the volume of the variety  , and this in turn is related to the probability that two of the eigenvalues of a GOE matrix are close.
, and this in turn is related to the probability that two of the eigenvalues of a GOE matrix are close.
